Research

[ ResearchGate] [ Google Scholar] [ ORCID] [arXiv] [MathSciNet]

“Nothing takes place in the world whose meaning is not that of some maximum or minimum” - Leonhard Euler

Comparing 4 Langevin diffusions and momentum method on Ackley function.

Left: Langevin diffusion on the contour lines of Ackley function. Right: Improved Langevin diffusion by Fang et al. (SPA 1997)

Left: Classical SA on a randomly generated 50-node TSP. Right: Discrete ISA on the same 50-node TSP.

Left: Classical SA on a randomly generated 500-node TSP. Right: Discrete ISA on the same 500-node TSP.

Stochastic Gradient Langevin Dynamics (SGLD) on Walker2d: falls over, inches itself forward

Stochastic Gradient Landscape Modified Langevin Dynamics (SGLMLD) on Walker2d: keeps stepping forward

Comparing 4 landscape-modified Metropolis-Hastings of an Ising model on a 50x50 box

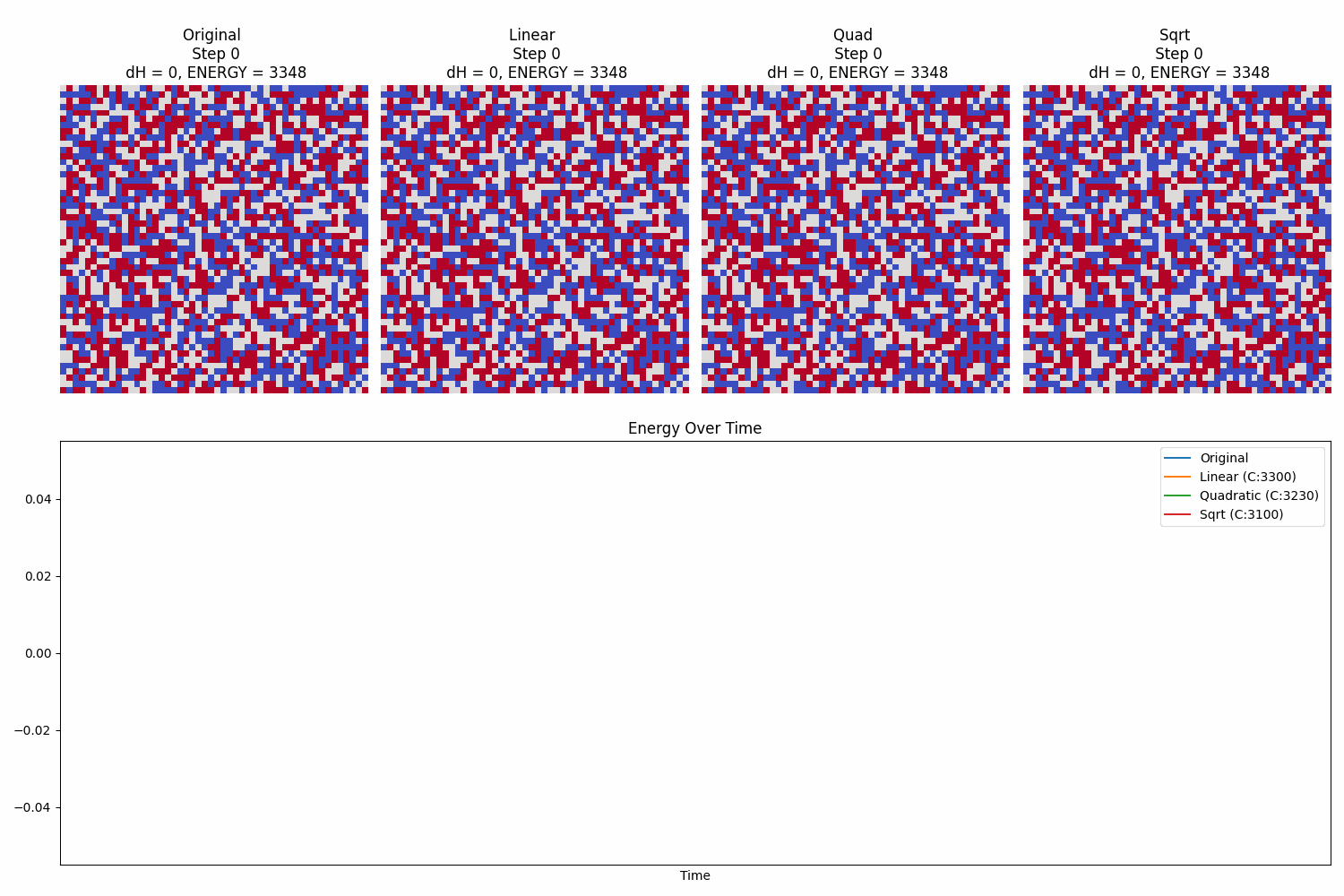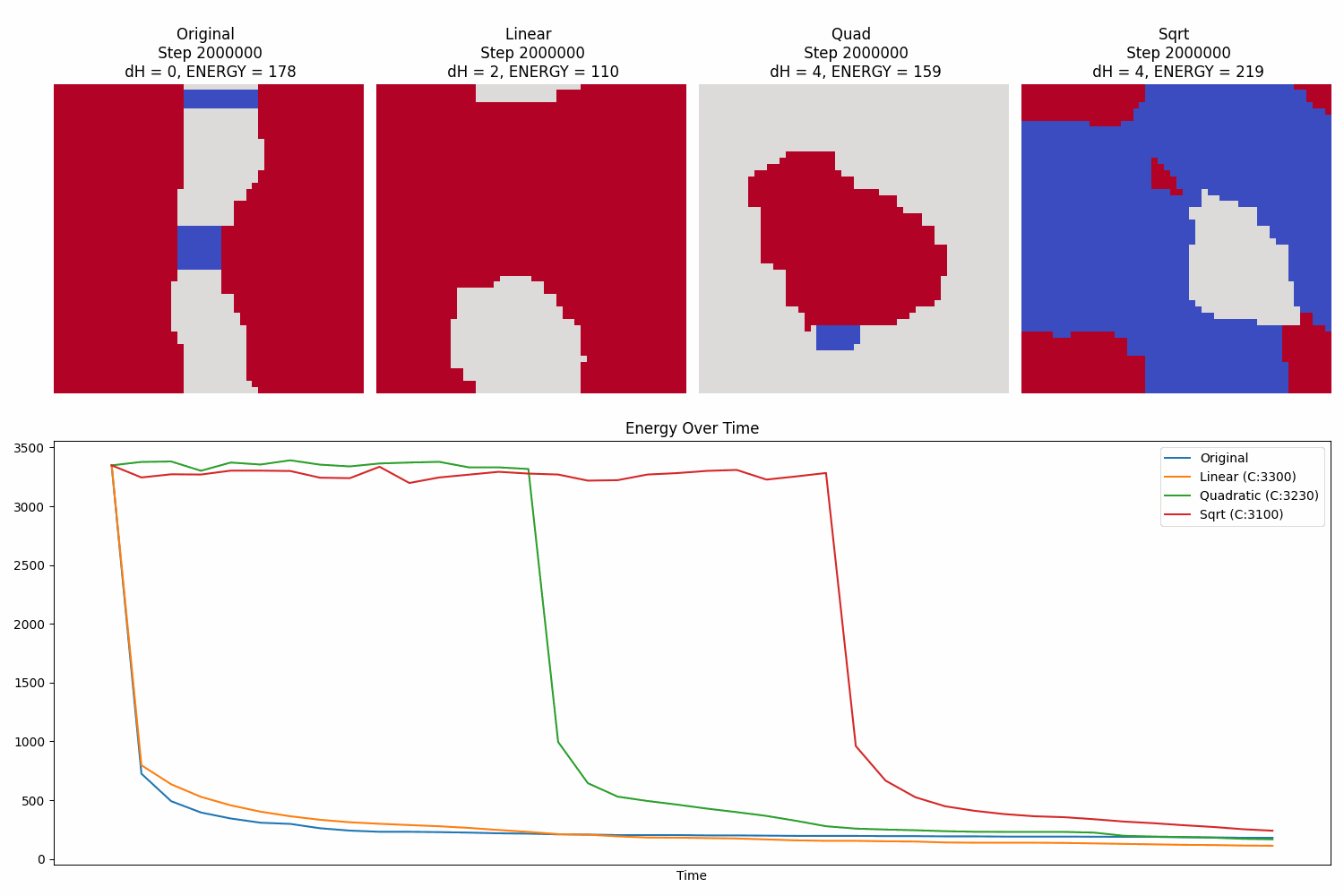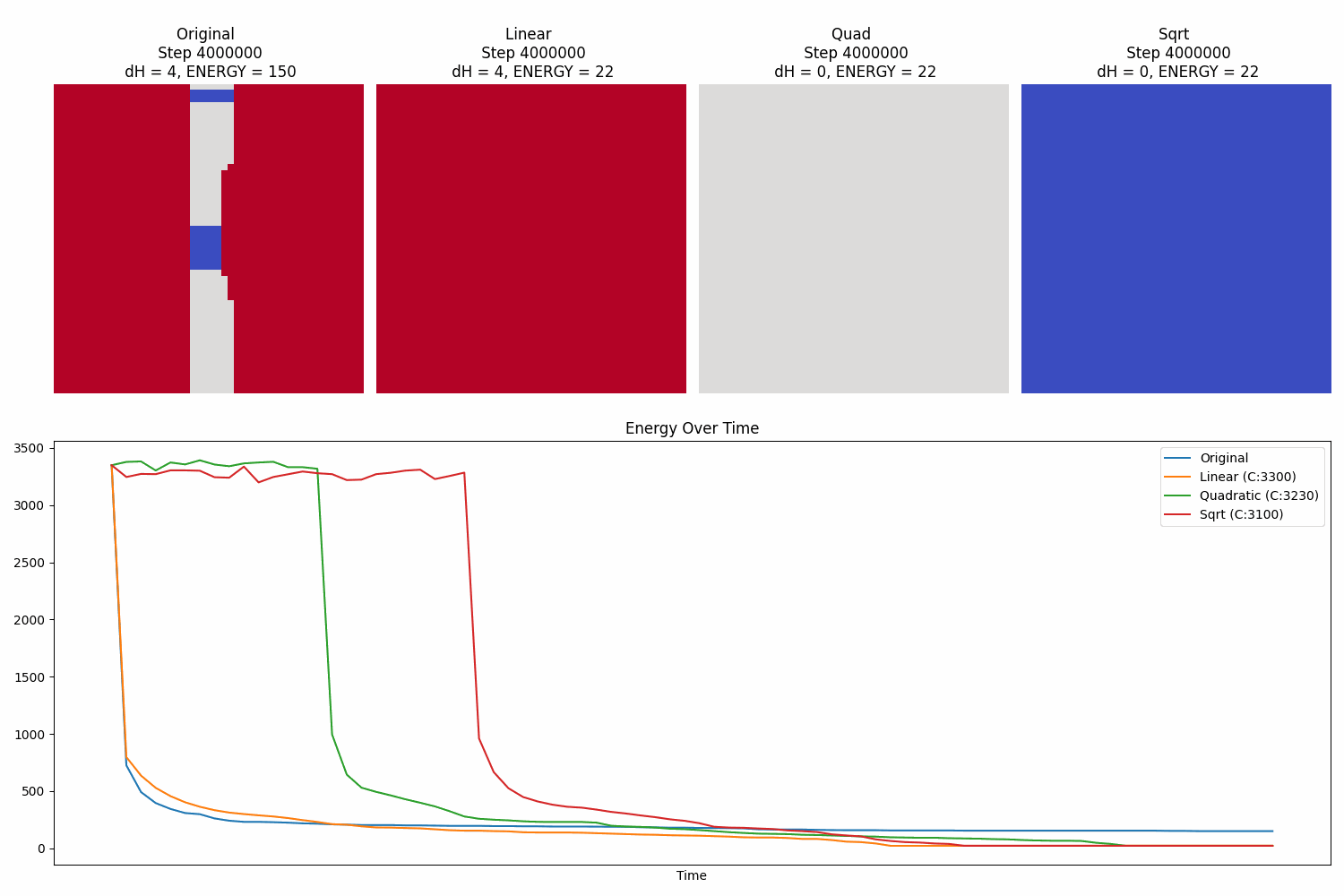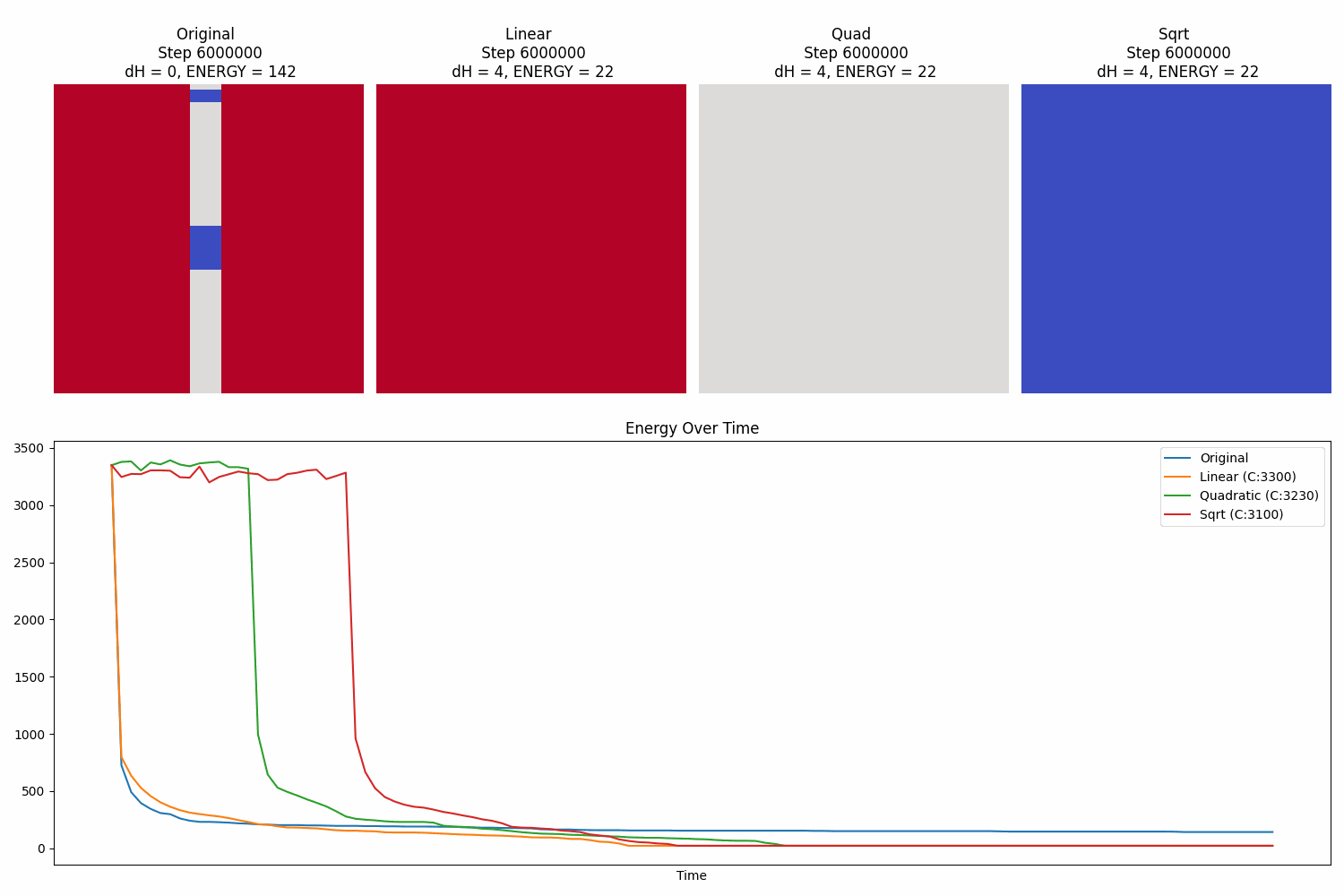
Comparing 4 landscape-modified Metropolis-Hastings of a 3-state Potts model on a 50x50 box

Research interests:

Markov chains, Markov processes: theory and applications
Stochastic algorithms: Markov chain Monte Carlo, Metropolis-Hastings, simulated annealing, Langevin dynamics, Hamiltonian Monte Carlo
Statistical physics, applied probability, theoretical computer science, stochastic optimization, Bayesian statistics, information theory

Preprints:

Ryan Zheyuan Lai and Michael C.H. Choi. Information-theoretic subset selection of multivariate Markov chains via submodular optimization. Submitted. [arXiv]

Youjia Wang and Michael C.H. Choi. Information-theoretic classification of the cutoff phenomenon in Markov processes. Submitted. [arXiv]

Michael C.H. Choi, Youjia Wang and Geoffrey Wolfer. Geometry and factorization of multivariate Markov chains with applications to the swapping algorithm. Submitted. [arXiv]

Michael C.H. Choi and Geoffrey Wolfer. Markov chain entropy games and the geometry of their Nash equilibria. Submitted. [arXiv] [ Slides]

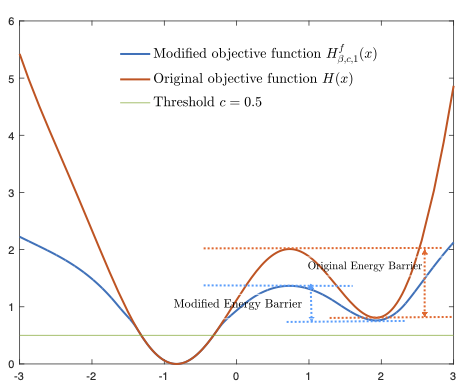
Michael C.H. Choi and Youjia Wang. [Improved Langevin Monte Carlo for stochastic optimization via landscape modification] (https://arxiv.org/abs/2302.03973). [arXiv]

Michael C.H. Choi and Jing Zhang. Improved annealing for sampling from multimodal distributions via landscape modification. [arXiv]

Michael C.H. Choi. On the convergence of an improved and adaptive kinetic simulated annealing. [arXiv] [ Slides] [ Youtube]

Publications:

Vitalii Kapitan and Michael C.H. Choi. Adaptive Gradient Scaling: Integrating Adam and Landscape Modification for Protein Structure Prediction. BMC Bioinformatics, to appear.

Michael C.H. Choi, Max Hird and Youjia Wang. Improving the convergence of Markov chains via permutations and projections. Random Structures and Algorithms, to appear. [arXiv] [ Youtube] [ Slides]

Michael C.H. Choi and Geoffrey Wolfer. Systematic approaches to generate reversiblizations of Markov chains. IEEE Trans. Inform. Theory (2024), Volume 70, Issue 5, pp. 3145-3161. [arXiv] [doi] [ Slides]

Michael C.H. Choi. Improved Metropolis-Hastings algorithms via landscape modifcation with applications to simulated annealing and the Curie-Weiss model. Adv. in Appl. Probab. (2024), Volume 56, Issue 2, pp. 587-620. [arXiv] [doi]

Michael C.H. Choi, Venkatkrishna Karumanchi. Landscape modification meets surrogate optimization: towards developing an improved stochastic response surface method. Proceedings of Winter Simulation Conference 2022. [ResearchGate]

Michael C.H. Choi, Zhipeng Huang. Generalized Markov chain tree theorem and Kemeny’s constant for a class of non-Markovian matrices. Statist. Probab. Lett. (2023), Volume 193, 109739. [ResearchGate][doi]

Michael C.H. Choi. Hitting, mixing and tunneling asymptotics of Metropolis-Hastings reversiblizations in the low-temperature regime. J. Math. Anal. Appl. (2021), Volume 497, Issue 1, 124853. [ResearchGate] [doi]

Michael C.H. Choi. An improved variant of simulated annealing that converges under fast cooling. Markov Process. Related Fields (2021), Volume 27, Issue 1, pp. 123-154. [Slides] [Handwritten notes] [arXiv] [doi]

Michael C.H. Choi, Pierre Patie. Analysis of non-reversible Markov chains via similarity orbit. Combin. Probab. Comput. (2020), Volume 29, Issue 4, pp. 508-536. [ Slides] [arXiv][doi]

Michael C.H. Choi, Chihoon Lee and Jian Song. Entropy flow and De Bruijn’s identity for a class of stochastic differential equations driven by fractional Brownian motion. Probab. Engrg. Inform. Sci., to appear. [arXiv][doi]

Michael C.H. Choi. Metropolis-Hastings reversiblizations of non-reversible Markov chains. Stochastic Process. Appl. (2020), Volume 130 Issue 2 Page 1041-1073. [ Slides] [arXiv][doi]

Michael C.H. Choi and Lu-Jing Huang. On hitting time, mixing time and geometric interpretations of Metropolis-Hastings reversiblizations. J. Theoret. Probab. (2020), Volume 33 Issue 2 Page 1144-1163. [arXiv][doi]

Michael C.H. Choi, Evelyn Li. A Hoeffding’s inequality for uniformly ergodic diffusion process. Statist. Probab. Lett. (2019), Volume 150 Page 23-28. [arXiv][doi]

Michael C.H. Choi. On resistance distance of Markov chain and its sum rules. Linear Algebra Appl. (2019), Volume 571 Page 14-25. [arXiv][doi]

Michael C.H. Choi, Pierre Patie. Skip-free Markov chains. Trans. Amer. Math. Soc. (2019), Volume 371 Number 10 Page 7301-7342. [arXiv][doi]

Michael C.H. Choi. Velocity formulae between entropy and hitting time for Markov chains. Statist. Probab. Lett. (2018), Volume 141 Page 62-67. [arXiv][doi]

Michael C.H. Choi. Hitting time and mixing time bounds of Stein’s factors. Electron. Commun. Probab. 23 (2018), paper no. 6. [arXiv][doi]

Michael C.H. Choi, Pierre Patie. A sufficient condition for continuous-time finite skip-free Markov chains to have real eigenvalues. Proceedings of AMMCS-CAIMS 2015.

Michael C.H. Choi, Eric C.K. Cheung. On the expected discounted dividends in the Cramer-Lundberg model with more frequent ruin monitoring than dividend decisions. Insurance Math. Econom. (2014) Volume 59 121-132. [doi]